1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
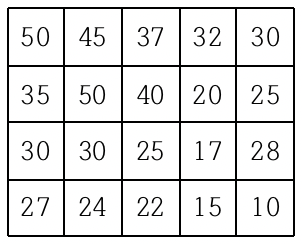
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
 |
 |
 |
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
예제 입력4 550 45 37 32 30 35 50 40 20 25 30 30 25 17 28 27 24 22 15 10 |
예제 출력3 |
풀이
목표 지점으로 내려가는 경우의 수를 찾는 문제이다.
일단, 현재 좌표에서 내려갈 수 있는 곳의 좌표를 무한정 찾는 방식으로 무작정 풀어보았다.
만약 현재 좌표에서 좌, 우로 내려갈 수 있다면 양쪽의 좌표를 후보 리스트에 저장하고
후보 리스트에 좌표가 남아있다면 계속해서 꺼내어 내리막 길을 찾는 방식으로 작성했다.
import sys
input = sys.stdin.readline
m,n = map(int,input().split())
g = [list(map(int,input().split())) for i in range(m)]
candidate,result = [[0,0]], 0
while(candidate):
i = candidate.pop()
if i == [m-1,n-1]:
result += 1
continue
if i[1] > 0 and g[i[0]][i[1]] > g[i[0]][i[1]-1]:
candidate.append([i[0],i[1]-1])
if i[1] < n-1 and g[i[0]][i[1]] > g[i[0]][i[1]+1]:
candidate.append([i[0],i[1]+1])
if i[0] > 0 and g[i[0]][i[1]] > g[i[0]-1][i[1]]:
candidate.append([i[0]-1,i[1]])
if i[0] < m-1 and g[i[0]][i[1]] > g[i[0]+1][i[1]]:
candidate.append([i[0]+1,i[1]])
print(result)
코드가 상당히 더럽지만 다행히 예제와 직접 짠 다른 예제들은 잘 풀렸다.
여담이지만 TLE를 상관하지 않고 올바른 답을 낼 수 있는 코드를 작성해놓는 것은 반례를 찾을 때 좋은 것 같다.
하지만 당연하게도 시간 초과에 걸리고 말았다.
이미 탐색했던 중복된 경로를 반복하여 탐색하기 때문이다.
바로 여기서 dp(다이나믹 프로그래밍)의 메모이제이션이 필요함을 알 수 있다.
만약, 이미 지나갔던 경로인데 목표 지점까지 도달했었던 경로라면
굳이 더 경로를 찾지 않아도 목표 지점까지 갈 수 있다는 말이 된다.
단, 그 경로에서 목표 지점까지 갈 수 있는 올바른 분기점이 몇 개인지 판별해야 한다.
무작정 분기점이 3개인 경로라고 3가지 경우가 더 있다고 판별해선 안 된다는 말이다.
문제를 해결하기 위해 dfs와 dp배열 두 가지를 활용할 것이다.
우선 dp는 지도와 똑같은 크기로 구성한다.
그리고 각각의 좌표에 들어갈 수는 -1, 0, 1이상의 수 로 나뉜다.
-1은 아직 한 번도 탐색하지 않은 좌표, 0은 목표 지점까지 올바른 경로가 없는 좌표를 의미한다.
그리고 목표 지점까지 갈 수 있는 좌표라면, 방문한 횟수에 따라 수가 올라갈 것이다.
이제 dfs로 목표 경로를 재귀로 탐색하며 위의 과정을 진행하면 된다.
필자는 문제와 반대되게, 정답인 목표지점부터 시작지점까지 오르막길로 탐색하는 순으로 진행했다.
import sys
input = sys.stdin.readline
# 재귀 제한을 풀어줘야 런타임 오류에 걸리지 않는다.
sys.setrecursionlimit(10**8)
m,n = map(int,input().split())
g = [list(map(int,input().split())) for i in range(m)]
dp = [[-1 for i in range(n)] for i in range(m)]
def dfs(x,y):
# 목표 지점에 도달했다면
if x == 0 and y == 0:
return 1
# 방문하지 않았던 경로라면
if dp[x][y] == -1:
dp[x][y] = 0
# 상하좌우 탐색을 시도한다
for i,j in (-1,0), (1,0), (0,-1), (0,1):
# 인덱스에 벗어나지 않고 오르막길이라면
if 0 <= x+i < m and 0 <= y+j < n and g[x+i][y+j] > g[x][y]:
dp[x][y] += dfs(x+i, y+j)
return dp[x][y]
print(dfs(m-1,n-1))'알고리즘 연습 > 동적 계획법 상급' 카테고리의 다른 글
| [🥇3 / 백준 7579 / 파이썬] 앱 (0) | 2021.08.02 |
|---|---|
| [🥇3 / 백준 10942 / 파이썬 ] 팰린드롬? (0) | 2021.07.28 |
| [🥇3 / 백준 11049 / 파이썬] 행렬 곱셈 순서 (2) | 2021.07.27 |
| [🥈1 / 백준 2293 / 파이썬] 동전 1 (0) | 2021.07.21 |
| [🥇3 / 백준 11066 / 파이썬] 파일 합치기 (0) | 2021.07.19 |