문제
조규현과 백승환은 터렛에 근무하는 직원이다.
하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다.
다음은 조규현과 백승환의 사진이다.
이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다.
조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.
조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고,
조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때,
류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
한 줄에 x1, y1, r1, x2, y2, r2가 주어진다.
x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고,
r1, r2는 10,000보다 작거나 같은 자연수이다.
출력
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다.
만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
예제 입력30 0 13 40 0 37 0 0 3 0 7 4 1 1 1 1 1 5 |
예제 출력2 1 0 |
풀이
주어진 입력을 바탕으로 아래와 같은 방정식을 구할 수 있다.
x2 + y2 = 132
(x-40)2 + y2 = 372
우선 그래프를 그려 확인해보았다.
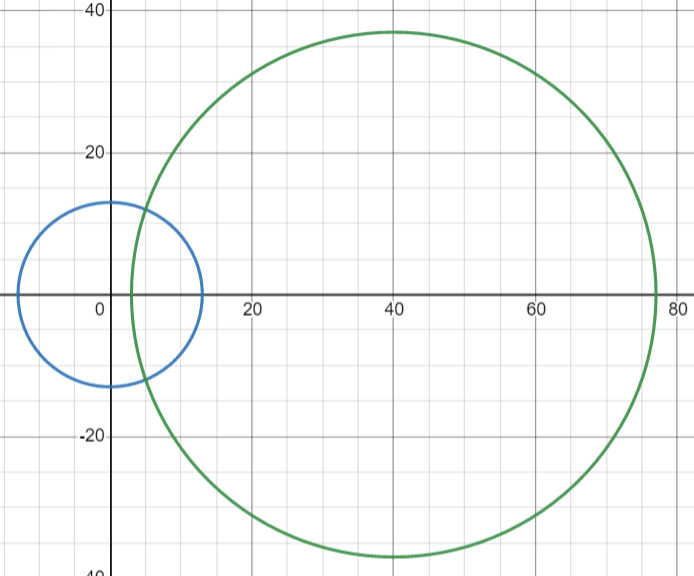
류재명이 있을 수 있는 위치의 수란, 두 원의 교점의 수 의미하는 것을 알 수 있다.
파란색 원의 반지름이 3이 된다면 아래와 같이 외접하게 된다.
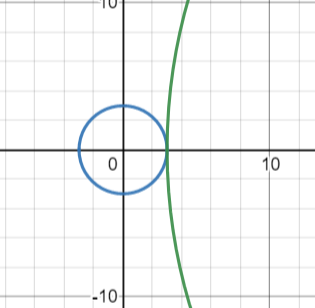
이 경우 류재명의 위치는 두 원이 외접하는 부분 한 곳뿐이다.
반대로 파란색 원의 반지름이 77로 내접하는 경우도 생길 수 있다.
여기서, 두 원 사이의 거리와 두 반지름의 합이 같거나, 차의 절댓값이 같다면
두 원은 서로 접한다는 사실을 알 수 있다.
그렇다면 자연스럽게 두 범위 이내는 교점이 두 개,
범위 밖은 교점이 없다는 사실도 추론할 수 있다.
접점이 무한대일 경우는 두 원이 일치할 경우뿐이니, 따로 예외처리를 해 주면 되겠다.
for i in range(int(input())):
a = list(map(int, input().split()))
b = [a.pop() for _ in range(3)]
b = b[::-1]
if a == b: # 두 원이 일치하는 경우
print(-1)
else:
d=((a[0]-b[0])**2 + (a[1]-b[1])**2)**0.5
# 두 원의 거리. 피타고라스 공식 이용
if d == a[2]+b[2] or d == abs(a[2]-b[2]):
print(1) # 두 원이 외접 혹은 내접하는 경우
elif d < a[2]+b[2] and d > abs(a[2]-b[2]):
print(2) # 두 원이 교차하는 경우
else:
print(0) # 그 외 서로 만나지 않는 경우
readline()을 사용해도 되지만, 성능 문제를 유발할 문제는 아니어서
그냥 input()을 사용했다.
'알고리즘 연습 > 수학, 정수론, 기하' 카테고리의 다른 글
| [🥉2 / 백준 1225 / 파이썬] 이상한 곱셈 (0) | 2021.07.18 |
|---|---|
| [🥉3 / 백준 1009 / 파이썬] 분산처리 (0) | 2021.07.08 |
| [백준 3053] 기본 수학 2 - 택시 기하학 (0) | 2021.05.30 |
| [백준 4153] 기본 수학 2 - 직각삼각형 (0) | 2021.05.30 |
| [백준 3009] 기본 수학 2 - 네 번째 점 (0) | 2021.05.30 |