1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
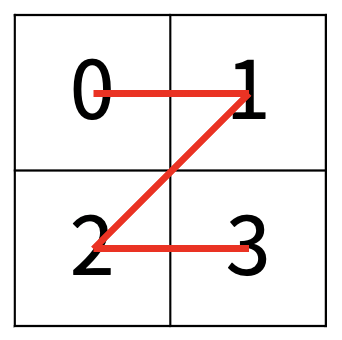
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.

N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
예제 입력 12 3 1
|
예제 출력 111
|
예제 입력 23 7 7
|
예제 출력 263
|
예제 입력 31 0 0
|
예제 출력 30
|
예제 입력 44 7 7
|
예제 출력 463
|
예제 입력 510 511 511
|
예제 출력 5262143
|
예제 입력 610 512 512
|
예제 출력 6786432
|
풀이
배열의 최대 크기가 2^30 로, 전체 탐색을 사용한다면 최대 약 10억번의 연산이 필요하다.
따라서 필요한 곳만 탐색하고 나머지는 빠르게 넘기기 위해 분할 탐색 알고리즘을 사용한다.
분할 탐색을 시행할 때 중요한 점은 재귀로 모든 부분을 분할하여 탐색하면 안 된다는 것이다.
그렇게 한다면 전체 탐색과 순서만 달라질 뿐이지, 결과적으로는 시간복잡도의 개선이 없다.

위 그림과 예제 1을 이용하여 문제를 풀어보겠다.
분할 탐색은 DP와 반대로 Top-Down 방식이다.
따라서 전체부터 시작하여 작은 부분으로 내려간다.
한 변의 길이는 2^2 이므로 4, 시작 지점인 (x,y)는 (0,0) 으로 진행한다.
이제 시작 지점에서 한 변의 길이를 더한 범위 내에 r과 c가 포함된다면 분할 탐색을 한다.
만약 포함하지 않는다면 변의 제곱을 반환하여 칸 수를 한 번에 계산한다.

범위 내에 (3,1)이 포함된다. 분할 탐색을 진행한다.

Z 방향대로 분할 탐색을 한다.
빨간색 테두리를 친 부분에 (3,1) 부분이 없으므로 한 변의 길이인 2의 제곱을 반환하여 칸 수를 한 번에 return한다.
그리고 다음 부분으로 넘어간다.

마찬가지로 범위 내에 (3,1)이 없으므로 칸 수를 return하고 다음으로 넘어간다.

마침내 (3,1) 좌표를 포함하게 되었다.
이미 2*2로 분할의 최소 범위이기 때문에 분할 탐색 대신 실제로 좌표를 세어주면 된다.
(x,y), (x,y+1), (x+1,y), (x+1,y+1) 순서로 진행하여 순서에 맞게 칸 수를 더해준 뒤 출력한다.
import sys
def dc(x,y,n):
global cnt
if x>r or x+n <= r or y>c or y+n <= c:
cnt += n**2
return
if n > 2:
n//=2
dc(x,y,n)
dc(x,y+n,n)
dc(x+n,y,n)
dc(x+n,y+n,n)
else:
if x==r and y==c:
print(cnt)
elif x==r and y+1==c:
print(cnt+1)
elif x+1==r and y==c:
print(cnt+2)
else:
print(cnt+3)
sys.exit()
n,r,c = map(int,input().split())
cnt = 0
dc(0,0,2**n)'알고리즘 연습 > 분할 정복' 카테고리의 다른 글
| [🏅2 / 백준 2261 / 파이썬] 가장 가까운 두 점 (0) | 2021.07.10 |
|---|---|
| [🏅5 / 백준 6549 / 파이썬] 히스토그램에서 가장 큰 직사각형 (0) | 2021.07.09 |
| [🥇3 / 백준 11444 / 파이썬] 피보나치 수 6 (0) | 2021.07.07 |
| [🥇4 / 백준 10830 / 파이썬] 행렬 제곱 (2) | 2021.07.07 |
| [🥉1 / 백준 2740 / 파이썬] 행렬 곱셈 (0) | 2021.07.06 |