2217번: 로프
N(1 ≤ N ≤ 100,000)개의 로프가 있다. 이 로프를 이용하여 이런 저런 물체를 들어올릴 수 있다. 각각의 로프는 그 굵기나 길이가 다르기 때문에 들 수 있는 물체의 중량이 서로 다를 수도 있다. 하
www.acmicpc.net
문제
N(1 ≤ N ≤ 100,000)개의 로프가 있다. 이 로프를 이용하여 이런 저런 물체를 들어올릴 수 있다. 각각의 로프는 그 굵기나 길이가 다르기 때문에 들 수 있는 물체의 중량이 서로 다를 수도 있다.
하지만 여러 개의 로프를 병렬로 연결하면 각각의 로프에 걸리는 중량을 나눌 수 있다. k개의 로프를 사용하여 중량이 w인 물체를 들어올릴 때, 각각의 로프에는 모두 고르게 w/k 만큼의 중량이 걸리게 된다.
각 로프들에 대한 정보가 주어졌을 때, 이 로프들을 이용하여 들어올릴 수 있는 물체의 최대 중량을 구해내는 프로그램을 작성하시오. 모든 로프를 사용해야 할 필요는 없으며, 임의로 몇 개의 로프를 골라서 사용해도 된다.
입력
첫째 줄에 정수 N이 주어진다. 다음 N개의 줄에는 각 로프가 버틸 수 있는 최대 중량이 주어진다. 이 값은 10,000을 넘지 않는 자연수이다.
출력
첫째 줄에 답을 출력한다.
예제 입력210 15 |
예제 출력20 |
풀이
주어진 로프를 사용하여 버틸 수 있는 최대 하중을 구하는 문제이다.
문제 이해만 제대로 한다면, 쉽게 풀 수 있는 문제이다.
즉, 코드 작성 난이도가 크게 어렵지 않다.
일단 각 로프가 버틸 수 있는 최대 무게들이 주어진다.
그리고 우리가 구해야 할 것은 최대 중량인 w이다.
중량 w를 들어올릴 때 각 로프에 걸리는 중량은 w/k(로프의 개수) 라고 했다.
그렇다면, 현재까지 사용한 로프들 중 가장 약한 것이 w/k 보다는 높아야 한다.
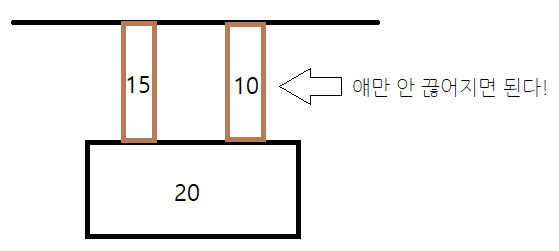
따라서, w/k(각각의 로프에 걸리는 중량)가 가장 약한 로프의 버틸 수 있는 무게와 같아질 때 w가 최대 하중이라고 할 수 있다.
즉,
w/k = 가장 약한 로프가 버틸 수 있는 무게
w = k * 가장 약한 로프가 버틸 수 있는 무게
위 공식이 성립하게 된다.
로프들을 내림차순으로 정렬하고, k * 현재 고른 로프의 최대 무게를 dp에 저장해주자(메모이제이션).
그리고, max(dp)를 출력하면 된다.
import sys
input = sys.stdin.readline
n = int(input())
rope = sorted([int(input()) for i in range(n)])[::-1]
dp = []
for i in range(n):
dp.append(rope[i]*(i+1))
print(max(dp))'알고리즘 연습 > 동적 계획법' 카테고리의 다른 글
| [🥈3 / 백준 11727 / 파이썬] 2×n 타일링 2 (0) | 2021.08.15 |
|---|---|
| [🥈3 / 백준 2193 / 파이썬] 이친수 (0) | 2021.08.15 |
| [🥈2 / 백준 9465 / 파이썬] 스티커 (0) | 2021.08.09 |
| [🥈4 / 백준 13699 / 파이썬] 점화식 (0) | 2021.07.26 |
| [🥈5 / 백준 14916 / 파이썬] 거스름돈 (0) | 2021.07.25 |