2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, <그림 1>과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
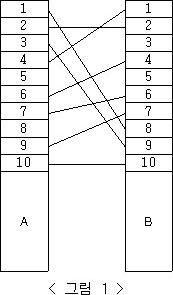
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
예제 입력81 8 3 9 2 2 4 1 6 4 10 10 9 7 7 6 |
예제 출력3 |
풀이
LIS 응용 문제이기 때문에 최대한 연관지어 생각하려 했다.
전봇대 B에 놓인 전깃줄들은 순서대로 1 2 4 6 7 8 9 10 이다.
하지만 A 전봇대에 뒤죽박죽 연결됨으로써 몇 가지 가지치기를 해야하는 상황이다.
만약 이 숫자가 그대로 순서대로 놓였다면 전깃줄은 정리할 필요가 없다.
바로 여기서 전봇대 A가 인덱스이고 전봇대 B가 숫자라고 한다면? 이라는 생각이 들었다.
여기서 이미 문제는 다 풀렸다. 왼쪽에 들어온 숫자를 기준으로 정렬하여 뒤 숫자들을 리스트에 넣고
이전의 수열 알고리즘을 활용하자.
n = int(input())
nums = [[0,0]] + [list(map(int,input().split())) for i in range(n)]
nums.sort()
temp = []
for i in nums:
temp.append(i[1])
nums = temp
dp = [0, 1]
cp = [0, nums[1]]
for i in range(2, n+1):
for j in range(len(cp)-1,-1,-1):
if nums[i] > cp[j]:
dp.append(j+1)
if j+1 < len(cp):
cp[j+1]=nums[i]
else:
cp.append(nums[i])
break
print(n-max(dp))'알고리즘 연습 > 동적 계획법' 카테고리의 다른 글
| [🥈2 / 백준 1912 / 파이썬] 연속합 (0) | 2021.06.19 |
|---|---|
| [🥇5 / 백준 9251 / 파이썬] LCS (0) | 2021.06.19 |
| [🥇3 / 백준 11054 / 파이썬] 가장 긴 바이토닉 부분 수열 (0) | 2021.06.16 |
| [🥈2 / 백준 11053 / 파이썬] 가장 긴 증가하는 부분 수열 (LIS(Longest Increasing Subsequence)) (0) | 2021.06.16 |
| [🥈1 / 백준 2156 / 파이썬] 포도주 시식 (0) | 2021.06.16 |