반응형
11401번: 이항 계수 3
자연수 \(N\)과 정수 \(K\)가 주어졌을 때 이항 계수 \(\binom{N}{K}\)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
자연수 N과 정수 K가 주어졌을 때 이항 계수 (NK)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 4,000,000, 0 ≤ K ≤ N)
출력
(NK)를 1,000,000,007로 나눈 나머지를 출력한다.
예제 입력5 2 |
예제 출력10 |
풀이
벌써 3번째 이항 계수 문제이다.
페르마의 소정리를 활용하는 문제인데, 알고리즘이 복잡하다기 보단 페르마의 소정리와 모듈러 연산에 대한 이해를 요하는 문제이다.
다시 이항 계수 공식을 보자.

최대 입력값은 4,000,000으로 팩토리얼을 계산하기엔 어마어마한 숫자이다.
따라서 조건에 따라 1,000,000,007 로 나누어주어야 한다.
편의상 1,000,000,007을 p라 하고, 이를 다시 공식으로 써 보면
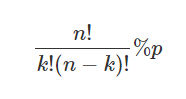
이같이 되는데 모듈러 연산은 분수꼴에 적용할 수 없다.
위 식을 계산하기 위해선 k!(n-k)! % p의 역원을 구해야 한다.
페르마의 소정리에 의해, 가 소수이고 a가 의 배수가 아니면
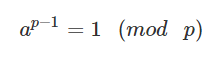
위 공식이 성립한다. 이를 변형하면
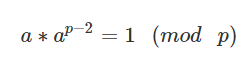

즉, (k!(n-k)!)-1 % p = (k!(n-k)!)p-2 % p 가 된다.
n, k = map(int,input().split())
P = 1000000007
def factorial(num, mod):
result = 1
for i in range(2, num+1):
result = result * i % P
return result
def power(num, p, mod):
if p == 1:
return num % mod
if p % 2:
return ((power(num,p//2,mod) ** 2) * num) % mod
else:
return (power(num,p//2,mod) ** 2) % mod
# 분할 정복은 이 거듭제곱에서 활용된다.
print(factorial(n, P) * power((factorial(k, P) * factorial(n-k, P)), P-2, P) % P)
반응형
'알고리즘 연습 > 분할 정복' 카테고리의 다른 글
| [🥇4 / 백준 10830 / 파이썬] 행렬 제곱 (2) | 2021.07.07 |
|---|---|
| [🥉1 / 백준 2740 / 파이썬] 행렬 곱셈 (0) | 2021.07.06 |
| [🥈1 / 백준 1629 / 파이썬] 곱셈 (0) | 2021.07.04 |
| [🥈2 / 백준 1780 / 파이썬] 종이의 개수 (0) | 2021.07.04 |
| [🥈1 / 백준 1992 / 파이썬] 쿼드트리 (0) | 2021.07.04 |