11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
문제
N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스가 M개 있다. 각 버스는 A, B, C로 나타낼 수 있는데, A는 시작도시, B는 도착도시, C는 버스를 타고 이동하는데 걸리는 시간이다. 시간 C가 양수가 아닌 경우가 있다. C = 0인 경우는 순간 이동을 하는 경우, C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우이다.
1번 도시에서 출발해서 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
출력
만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다. 그렇지 않다면 N-1개 줄에 걸쳐 각 줄에 1번 도시에서 출발해 2번 도시, 3번 도시, ..., N번 도시로 가는 가장 빠른 시간을 순서대로 출력한다. 만약 해당 도시로 가는 경로가 없다면 대신 -1을 출력한다.
예제 입력 13 41 2 4 1 3 3 2 3 -1 3 1 -2 |
예제 출력 14 3 |
예제 입력 23 41 2 4 1 3 3 2 3 -4 3 1 -2 |
예제 출력 2-1 |
예제 입력 33 21 2 4 1 2 3 |
예제 출력 33-1 |
풀이
특정 정점에서 각 정점까지의 최단 거리를 구하되, 음수 간선이 있을 경우를 고려하는 문제이다.
다익스트라의 경우 O(ElogE)로 최단 거리를 구할 수 있는 좋은 알고리즘이지만,
음수 간선이 있을 경우에는 사용할 수가 없다.
정확히는 음수 간선이 있을 경우 음수 사이클이 있을 수 있으므로 사용할 수 없다.
이유를 아래에서 살펴보도록 하자.
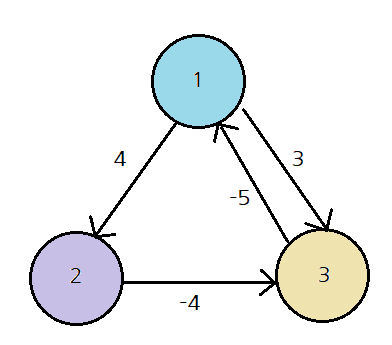
위 그림은 예제 2의 변형이다.
정점 1에서 2와 3까지의 최단 거리를 구한다고 가정한다.
3까지의 최단 거리는 1 → 2 → 3 이다.2까지의 최단 거리는? 자세히 보면 1과 3이 사이클을 형성하고 있는 것을 알 수 있다.그런데 음수 간선의 크기가 더 크므로 1과 3의 사이클을 반복한다면 계속하여 거리가 줄어들게 된다.이렇게 음수 사이클에 갇혀 무한 루프에 빠지게 되는 것이다.
음수 사이클이 없더라도 문제는 발생할 수 있다.다익스트라는 기본적으로 heap 자료구조를 이용하여 '방문하지 않은 정점을 방문할 때 중 가중치가 가장 낮은 간선'을 이용한다.
따라서 아래와 같은 그래프일 경우 힙에 1 → 3 간선이 먼저 진행이 되어 3을 이미 방문했기 때문에1 → 2 → 3 이라는 최단경로를 무시하게 될 수 있다.
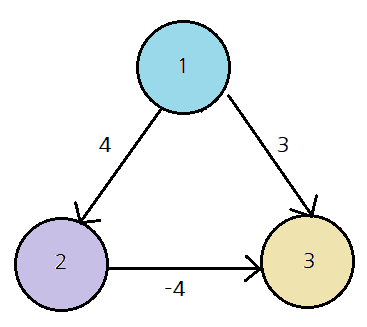
이는 다익스트라를 개선하여 해결할 수도 있지만,어차피 음수 사이클을 해결하기 어렵기 때문에 그다지 적합하지 않은 알고리즘이라고 할 수 있다.
따라서 이러한 문제를 해결하기 위해 음수 가중치에도 무사히 최단 경로를 구할 수 있는 벨만-포드(Bellman-Ford) 알고리즘을 사용한다.
벨만 포드 알고리즘은 최단 경로의 최대 길이가 V-1 임을 이용한 알고리즘이다. (V : 정점의 수)입력받은 간선을 이용해 탐색을 V-1번 진행한다.음수 간선이 있다 하더라도 모든 경우의 수를 훑기 때문에 무사히 최단 거리를 도출해낼 수 있다.
이제 음수 사이클이 있나 확인해야 한다.정상적인 최단 경로 도출은 V-1 번 반복했을 때 '무조건' 이루어져야 한다.따라서 전체 탐색을 한 번 더 진행하여, 만약 탐색이 이루어진다면 음수 사이클이 존재하는 것이다.
이 문제에서는 음수 사이클이 존재할 경우 -1만을 출력하라고 했으므로 -1을 출력한 뒤 종료하면 된다.
다만 벨만-포드 알고리즘은 전체 탐색을 진행하기 때문에 시간복잡도가 O(VE)에 해당하므로 다익스트라보다 좋지 않다.음수 가중치가 존재할 때에만 적절히 활용해주도록 하자.
import sys
input = sys.stdin.readline
n,m = map(int,input().split())
graph,dist = [],[float('inf')] * n
dist[0] = 0
# 그래프 입력
for _ in range(m):
u,v,w = list(map(int,input().split()))
graph.append([u-1,v-1,w])
# V-1 번 탐색
for _ in range(n-1):
for u,v,w in graph:
if dist[v] > dist[u]+w:
dist[v] = dist[u]+w
# 음수 사이클 확인
for u,v,w in graph:
if dist[v] > dist[u]+w:
print(-1)
sys.exit()
for i in dist[1:]:
print(i if i != float('inf') else -1)'알고리즘 연습 > 최단 경로' 카테고리의 다른 글
| [🥇4 / 백준 1956 / 파이썬] 운동 (0) | 2021.09.10 |
|---|---|
| [🥇4 / 백준 11404 / 파이썬] 플로이드 (0) | 2021.09.08 |
| [🥇5 / 백준 1916 / 파이썬] 최소비용 구하기 (0) | 2021.09.01 |
| [🥇2 / 백준 9370 / 파이썬] 미확인 도착지 (0) | 2021.08.28 |
| [🥇4 / 백준 1504 / 파이썬] 특정한 최단 경로 (0) | 2021.08.27 |