반응형
2263번: 트리의 순회
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
www.acmicpc.net
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
예제 입력3
1 2 3 1 3 2 |
예제 출력2 1 3
|
풀이
후위 순회(포스트오더)의 마지막 노드가 중위 순회(인오더)의 루트 노드가 됨을 이용하여 풀어야 한다.
다음과 같은 이진 트리가 있다고 가정한다.
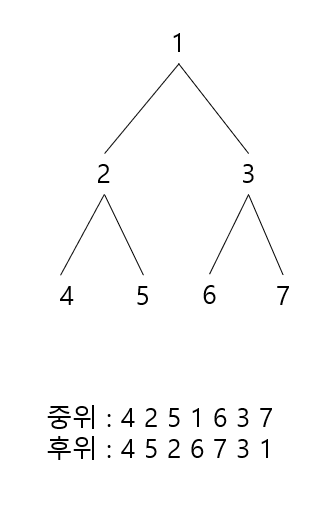
후위 순회의 마지막 노드인 1이 최상단 루트로, 중위 순회의 가운데에 있음을 알 수 있다.
이것을 기점으로 중위의 왼쪽과 오른쪽으로 분할하여 생각할 수 있다.
이는 현재 노드가 리프 노드가 아니라면 재귀적으로 반복이 가능하므로 분할 정복을 사용할 수 있다는 의미이다.
분할 정복을 위한 매개변수가 중위 순회의 시작과 끝, 후위 순회의 시작과 끝 총 4개 필요하다.
개인적으로 중위 순회의 시작과 끝은 분할만 하면 돼서 구하기 쉬웠지만, 후위 순회의 시작과 끝을 생각하는 것이 어려웠다.
키워드는 '크기'이다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**8)
n = int(input())
in_order = [-1]+list(map(int,input().split()))
post_order = [-1]+list(map(int,input().split()))
# 인오더를 분할하기 위해 매번 n번 탐색하면
# 시간 초과가 발생할 것이므로 미리 위치를 저장해준다.
pos = [-1]*(n+1)
for i in range(n+1):
pos[in_order[i]] = i
ans = []
def daq(in_start,in_end,post_start,post_end):
if (in_start > in_end) or (post_start > post_end):
return
root = post_order[post_end]
size = pos[root] - in_start
ans.append(root)
daq(in_start, pos[root]-1, post_start, post_start + size - 1)
daq(pos[root]+1, in_end, post_start + size, post_end - 1)
daq(1,n,1,n)
print(*ans)반응형
'알고리즘 연습 > 트리' 카테고리의 다른 글
| [🥇4 / 백준 4803 / 파이썬] 트리 (0) | 2022.04.11 |
|---|---|
| [🥇5 / 백준 1068 / 파이썬] 트리 (0) | 2022.01.30 |
| [🥈1 / 백준 1991 / 파이썬] 트리 순회 (0) | 2021.12.04 |
| [🥇3 / 백준 1167 / 파이썬] 트리의 지름 (2) | 2021.10.05 |
| [🥇4 / 백준 1967 / 파이썬] 트리의 지름 (0) | 2021.10.05 |